Деление с остатком в столбик для 5 класса с примерами

Алгоритм деления в столбик без остатка

Теперь покажите ребенку на примере о конфетах алгоритм вычисления.

• Возьмите чистый лист бумаги/тетрадь и напишите цифры 96 и 8.
• Разделите их перпендикулярными линиями.

• Покажите наглядно элементы.
• Укажите на то, что результат вычисления записывается под «делителем», а вычисления – под «делимым».
• Предложите маленькому ученику посмотреть на число 96 и определить цифру, которая больше 8.
• Из двух цифр 9 и 6, такой цифрой окажется 9.
• Спросите ребенка, сколько цифр 8 может «уместиться» в 9. Малыш, помня таблицу умножения, легко определит, что только раз. Поэтому запишите цифру 1 под подчеркиванием.
• Далее, умножьте делитель 8 на результат 1. Полученную цифру 8 запишите под первой цифрой делимого числа.
• Между ними поставьте знак «вычитания», и подведите итог. То есть, если от 9 отнять 8 получиться 1. Запишите результат.

На этом этапе объясните ребенку, что результат вычитания всегда должен быть меньше делителя. Если вышло наоборот, значит, малыш неправильно определил сколько 8 содержится в 9.

• Попросите снова ребенка определить цифру, которая больше делителя 8. Как видим, число 1 меньше 8. Поэтому нам следует объединить его со следующей цифрой делимого числа – 6.
• Припишите к единице 6 и получите 16.
• Далее, спросите у малыша сколько 8 содержится в 16. Правильный ответ 2 добавьте к первому.

• Снова умножьте 8 на 2. Полученный результат запишите под цифру 16.
• Путем «вычитания» (16-16) мы получим 0, что говорит о том, что наш результат вычисления – 12.

Далеко не все дети понимают деление и умножение с первого раза, поэтому родителям приходится дома подробнее разбирать эти процессы. Сегодня расскажем, как это сделать проще для ребенка. В книге объяснения строятся на визуальных принципах. Так школьнику будет понятнее, а родителю легче построить общение.

Что делать, если разделить нужно десятичную дробь?

Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.

Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.

Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.

Как научиться делить столбиком

Деление столбиком с остатком и без него нельзя начинать без подготовки. Сначала ребенок должен хорошо уметь и знать следующее:

• Разряды натуральных чисел (десятки, сотни, тысячи). Находить их в ряду многозначных цифр.
• Таблица умножения. Этот материал лучше выучить наизусть и постоянно повторять.
• Отнимать, складывать многозначные числа.
• Решать маленькие задачи на умножение, разность, сумму устно.

Отработайте все обозначенные умения до автоматизма. Затем приступайте к делению маленьких цифр на примере таблицы умножения в уме. Например, ребенок выучил, как умножать цифру 6:

6х2=12

6х3=18

6х4=24 и так далее.

Смело предлагайте такие примеры:

24:6=4

24:4=6

12:2=6

18:3=6

Через пару уроков школьник будет выполнять такие задания легко. Можно разнообразить занятия по устному счету играми на деление.

Игровые задания

Интересные математические игры на деление помогают детям закрепить навык, узнать законы работы с цифрами, освоить устный счет.

• Головоломки на развитие внимания. Напишите в тетради 3–5 примеров на деление с ответами. Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные с помощью устного счета.
• Подбор примера по результату. Предлагайте малышу ответ без примера. Давайте задание придумать задачу. Например, ответ 8. Ребенок может придумать такую задачу: 48:6.
• «Идем в магазин». Расставьте на полу игрушки с карточками. На листах написаны примеры: 6:2, 18:3, 42:7, 100:50. Игрушки — это «товар» в фантазийном магазине, частное после решения примера — их цена. Чтобы узнать стоимость покупки, нужно решить задания, а потом оплатить полученный результат в кассу. Играть лучше в небольшой команде — 2–3 человека.
• «Молчуны». Ребенок получает карточки с цифрами от 1 до 100. Задавайте вопросы с примерами на деление, ученик должен отвечать без слов, показывая правильный ответ.
• Небольшие самостоятельные работы с подарком за старательность. Распечатайте карточки с примерами в количестве 5–10 штук. Укажите время на решение, например 5 минут. Поставьте перед ребенком песочные часы. После выполнения контрольной верно поощрите школьника походом в зоопарк, кино, покупкой книги, сладостей.
• «Ищем дерево». Нарисуйте небольшой сад с деревьями на картоне. Каждому растению дайте номер, пусть их будет 10. На листочке для ученика напишите 3 примера:

45:9           120:60          14:7

Школьник должен вычислять результат к каждому заданию, а потом складывать все числа между собой.

Получится так:

45:9=5

120:60=2

14:7=2

5+2+2=9

Ребенок должен найти дерево под номером 9.

Для игры можно использовать цветные пуговицы и ставить их на занятые деревья. Развлечение подходит для командных соревнований.

После устной работы с делением натуральных чисел можно показать ребенку порядок записи примеров столбиком.

Если педагогического опыта у вас нет, посмотрите видеоурок на эту тему, вспомните теорию сами.

Теперь можно приступать к объяснению сложного материала школьнику. Есть несколько методик домашнего обучения делению:

1. Мама-учитель

Родителям придется ненадолго стать педагогами. Оборудовать доску, купить мел или маркеры. Заранее вспомнить школьный материал. Объяснить пошагово теорию и закрепить ее на практике с помощью большого количества самостоятельных, карточек, контрольных работ.

Например, это:

Затем нужно обсуждать с малышом материал, закреплять навык на практике несколько недель.

3. Нанять репетитора

Деление не самая сложная тема в школьной программе. В начальных классах можно легко обойтись без платных уроков с педагогом. Этот вариант оставим на крайний случай.

Деление натуральных чисел с остатком: правила, примеры и решения.

От общего представления о делении натуральных чисел с остатком будем двигаться дальше, и в этой статье мы разберемся с принципами, по которым проводится это действие. Вообще деление с остатком имеет много общего с делением натуральных чисел без остатка, так что мы будем часто ссылаться на материал указанной статьи.

Сначала разберемся с делением натуральных чисел с остатком в столбик. Дальше мы покажем, как можно отыскать результат деления натуральных чисел с остатком, проводя последовательное вычитание. После этого перейдем к методу подбора неполного частного, не забывая при этом приводить примеры с подробным описанием решения. Далее запишем алгоритм, позволяющий проводить деление натуральных чисел с остатком в общем случае. В конце статьи мы покажем, как выполняется проверка результата деления натуральных чисел с остатком.

Навигация по странице.

Как проводится

Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.

Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:

5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.

Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета.

Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.

Основные этапы:

1. Правильная запись. Делимое (17) – располагается по левую сторону. Правее от него пишут делитель (5). Между ними чертят вертикальную черту (обозначает знак деления), а затем, от этой черты ведут горизонтальную, выделяя делитель. Основная черта обозначена оранжевым цветом.
2. Поиск целого. Далее, выполняют первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой. 3 – это неполное частное (НЧ).
3. Определение остатка (ост-ка). 3*5=15. 15 подставляем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2. Указываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.

При делении таким образом, остаток всегда должен быть меньше делителя.

Скачать карточки

В качестве домашнего математического тренажера используйте карточки с примерами. В них включайте разные случаи: с однозначными и многозначными числами, деление с полным результатом и остатком. Скачать карточки можно бесплатно. Раздаточный материал обязательно следует напечатать для проверочной работы.

Ошибки с делением у детей в начальной школе встречаются довольно часто. Уделите этой теме максимум внимания и времени, чтобы усвоение последующего материала проходило без запинок. Используйте карточки, видеоуроки, постоянную тренировку навыка и повторение пройденных тем в игровой форме. Тогда домашние уроки не навеют на ребенку скуку и пройдут с максимальной пользой.

Понравился наш контент? Подпишитесь на канал в .

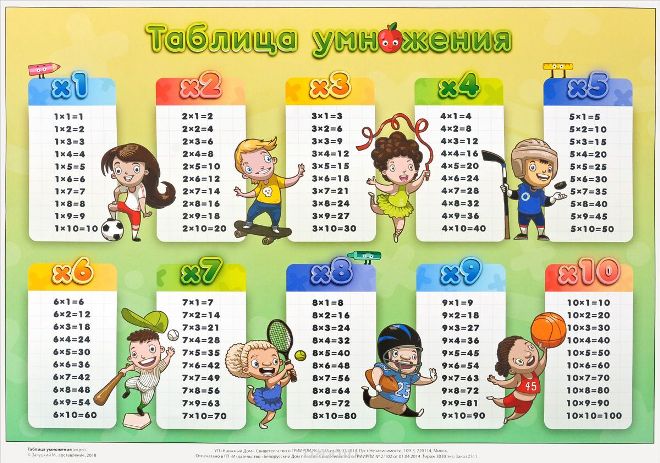
Обучение при помощи таблицы умножения

Пятиклассники быстро освоят арифметическое действие деление, если усвоили, как нужно умножать.

Обратите внимание ребенка на то, что процесс деления имеет связь с таблицей Пифагора. Для этого достаточно привести пример:

1. Попросите ученика умножить 8 на 5.
2. Поясните, что 40 – результат умножения 8 на 5.
3. Если разделить 40 на 8, в результате получаем 5. Следует объяснить ученику, что деление – это действие, обратное умножению.

Используйте в обучении таблицу Пифагора. Если взять число после знака равенства и разделить на число, которое стоит по другую строну знака, то получим третье число в примере.

Деление на двузначное число

Когда ученик 3-го класса усвоил деление на однозначное число, можно приступать к следующему этапу — работе с двузначными цифрами. Начинайте с простых, явных примеров, чтобы малыш понял алгоритм действий. Например, возьмите числа 196 и 28 и объясните принцип:

1. Сначала подберите примерное число для ответа. Для этого выясните приблизительно, сколько цифр 28 поместится в 196. Для удобства можно округлять оба числа: 200:30. Получится не больше 6. Полученное число не нужно записывать, это только догадка.
2. Проверяем результат умножением: 28х6. Получается 196. Предположения оказались верными.
3. Запишите ответ: 196:28 =6.

Еще один вариант обучения: деление на двузначное число уголком. Такой способ больше подходит для работы с числами от четырех разрядов, то есть тысяч. Приведем простой пример:

Напишите на листе бумаги 4070, начертите уголок и подпишите делитель — 74.
Определите, с какого числа начнете делить. Спросите у ребенка, можно ли разделить 4 на 74, 40? В результате малыш поймет, что сначала нужно ограничиться числом 407. Очертите полученную цифру сверху полукругом. 0 останется в стороне.
Теперь нужно выяснить, сколько 74 поместится в 407. Действуем с помощью логики и проверки умножением. Получится 5. Записываем результат под уголком (под делителем).
Теперь умножаем 74 на 5 и записываем результат под делимым. Получится 370

Важно начинать запись с первого числа слева.

После записи нужно подвести горизонтальную черту и отнять 370 от 407. Получится 37.
37 разделить на 74 нельзя, поэтому вниз сносится оставшийся в верхнем ряду 0.
Теперь делим 370 на 74

Подбираем множитель (5) и записываем его под уголком.
Умножаем 5 на 74, записываем результат в столбик. Получится 370.
Опять получаем разность. Результат будет равен 0. Значит, деление считается завершенным без остатка. 4070:74=55. Частное смотрим под уголком.

Для проверки правильности решение произведите умножение: 74х55=4070.

Деление столбиком с остатком

Пусть нам требуется разделить 1340 на 23.

Определяем неполное делимое – это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:

Сносим следующую цифру делимого – 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:

Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:

1340 : 23 = 58 (остаток 6)

Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток – 3:

3 : 10 = 0 (остаток 3)

Алгоритм деления столбиком на двузначное число

Объяснить ребенку деление на двузначное число можно на следующем примере: разделим 876 на 24.

1. Сделаем прикидку: 800 ÷ 20 = 40. Это значит, что в ответе должно получиться число, близкое к 40.
2. Точно так же, как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к более мелким.
3. Число сотен является однозначным, поэтому делим 87 на 24. Получается 3 десятка. 3 × 24 = 72. При вычитании от 87 получаем 15 десятков и еще 6 единиц – это число 156. Если его разделить на 24, получим 6 и 12 в остатке. Итак, 876 ÷ 24 = 36 (ост. 12).

Алгоритм деления на двузначное число выглядит следующим образом:

1. Сделать прикидку.
2. Найти первое неполное делимое.
3. Определить количество цифр в частном.
4. Найти цифры в каждом разряде частного
5. Найти остаток, в случае, если он есть.

Как делить столбиком меньшее число на большее?

девочка-школьница устала от решения примеров на деление столбиком

При таком делении у вас частное будет начинаться с 0 и иметь после него запятую.

Чтобы ребёнок лучше усвоил подобное деление и не запутался в количестве нулей, месте постановки запятой в частном, дайте ему такой пример:

• первое действие на вычитание проведите с нулями, записанными по одному под делителем и в графе «частное»,
• поставьте запятую в частном, а остатка после разницы добавьте ноль и продолжайте обычное деление в столбик,
• когда остаток от вычитания опять будет меньше делителя, допишите первому ноль и продолжайте действие. Финальный итог — получение ноля от разницы верхнего и нижнего чисел либо повторения остатка. В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.

Ниже пример.

примеры деления столбиком меньшего числа на большее

Деление с остатком

Деление с остатком подразумевает, что нацело число поделить не удалось и осталась какая-то часть, которая меньше делителя и которую разделить нельзя.

Где это может пригодиться в реальной жизни? Представим себе вполне реальную ситуацию: мы покупаем в магазине конфеты батончики по 38 рублей. Всего у нас 200 рублей, сколько сдачи нам должны дать?

Очевидно, что ровное количество конфет купить не получится, поскольку 200 на 38 нацело не поделится, но и конфету пилить в магазине не будут. Значит, остаток от 200 нам должны будут вернуть в виде сдачи.

$200:38=5 (ост.10)$ – именно 10 рублей остатка и будут сдачей, которую нам должны вернуть.

Долгое время только такие вычисления и производились, до тех пор, пока не возникла надобность в точных расчетах. Тогда на смену делению с остатком пришли десятичные дроби.

Делим десятичные дроби на 1000, 100, 10: как это сделать правильно?

Исходя из имеющихся и известных правил деления так называемых «обыкновенных дробей», деление на числа с нулями равносильно умножению. Необходимо перенести запятую на нужное количество цифр. Если значений не хватает, нули просто добавляются. Это же происходит с бесконечными десятичными дробями.

Поэтому, чтобы верно произвести действие деления десятичной дроби на числа с нулями, нужно перенести запятую на столько цифр, сколько нулей стоит после единицы в делителе: если это число 10 – то нуль один, если 100 – то два. И так далее.

Делим десятичные дроби на 1000, 100, 10

Примеры с бесконечными дробями решаются также:

Делим десятичные дроби на 1000, 100, 10

Деление двух десятичных дробей

Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.

Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.

Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.

В качестве примера: 28,4 делим на 3,2:

• Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
• Их полагается разделить. Причем сразу все число 284 на 32.
• Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
• Деление целой части закончилось, и в ответ полагается поставить запятую.
• Снести к остатку 0.
• Снова взять по 8.
• Остаток: 24. К нему приписать еще один 0.
• Теперь брать нужно 7.
• Результат умножения — 224, остаток — 16.
• Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.

Деление закончено. Результат примера 28,4:3,2 равен 8,875.

Разбор примеров на деление столбиком на двузначное число

Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.

Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.

Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.

Значение частного чисел 265 и 53 равно 5.

Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.

В частном будет однозначное число. 

Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.

Значение частного чисел 184 и 23 равно 8.

Рассмотрим более сложные случаи деления.

Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.

Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.

Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.

 Значение частного чисел 768 и 24 равно 32.

Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.

Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.

Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое  414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.

Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.

Значение частного чисел 15344 и 56 равно 274.

Почему нельзя делить на 0

Большинство школьников просто заучивают правило о том, что на 0 не делят. Интересно знать, почему. Оказывается, что из четырех математических действий – сложение, вычитание, умножение деление – математики признают полноценными только два – сложение и умножение. Эти операции включаются в само понятие числа, а остальные действия вытекают из них.

Например, запись 6 ÷ 3 можно понимать как результат того, что 6 предметов раскладывают на 3 части. В действительности это сокращенная форма уравнения 3 × Х = 6. То есть находим такое число, которое при умножении на 3 даст 6. Теперь становится понятно, почему на 0 не делят. Запись 4 ÷ 0, это сокращение от 0 × X = 4. Это задание подразумевает, что найденное число должно при умножении на 0 давать 4.

Есть правило, что, умножая на 0, мы всегда получаем 0. Таким образом, такого числового значения не существует, значит, задача не имеет решения, если быть более точными, не имеет смысла. Может возникнуть вопрос, можно ли 0 разделить на 0. Если мы запишем уравнение 0 × X = 0, то это уравнение можно решить. Например, если X = 0, то 0 × 0 = 0.

Попробуем взять X = 1, получим 0 × 1 = 0. Верно, значит 0 ÷ 0 = 1. Но так же может подойти равенство 0 ÷ 0 = 4, 0 ÷ 0 = 654 и т. д. Таким образом, можно брать любое число. В таком случае, мы не можем точно сказать, какому числу соответствует запись 0 ÷ 0. Поэтому эта запись не имеет смысла и получается, что на 0 не делится даже 0. Чтобы знать, как правильно производить деление, нужно запомнить, что на 0 не делят.

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Копилка»

Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение перезагрузка»

Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу

В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.